Trong bối cảnh cách mạng công nghiệp 4.0 và sự phát triển mạnh mẽ của trí tuệ nhân tạo (AI), Khoa học dữ liệu (Data Science) đang nổi lên là một trong những lĩnh vực có tiềm năng phát triển lớn nhất. Các công ty, tổ chức hiện đại đều dựa vào dữ liệu để ra quyết định chiến lược, tối ưu hóa quy trình và tạo ra giá trị cạnh tranh.

Hình 1. Ma trận kết nối – Khi Toán học gặp Dữ liệu
Tuy nhiên, đằng sau các mô hình dự đoán mạnh mẽ, các thuật toán máy học tinh vi và biểu đồ bắt mắt chính là nền tảng của toán học. Toán học không chỉ giúp một nhà khoa học dữ liệu hiểu rõ “tại sao” mô hình hoạt động, mà còn giúp cải tiến và áp dụng chúng một cách hiệu quả.
- Tầm quan trọng của toán học trong Khoa học dữ liệu
Hình 2. Bức tường toán học – Vũ trụ của các công thức và hình học
Nhiều người nghĩ rằng học Data science chỉ cần giỏi lập trình và biết dùng các công cụ như Python, SQL, hoặc R. Tuy nhiên, khi đi sâu hơn, để hiểu cách hoạt động của các mô hình học máy như hồi quy tuyến tính, cây quyết định, mạng nơ-ron nhân tạo hay phân cụm K-means, toán học chính là công cụ giúp bạn “tháo tung” các thuật toán để kiểm soát và tối ưu chúng.
Ví dụ, khi mô hình của bạn không học tốt (underfitting), bạn cần hiểu cách thay đổi hàm mất mát để cải thiện khả năng học. Khi thuật toán bị kẹt ở điểm cực tiểu cục bộ, bạn cần nắm vững bản chất của đạo hàm và gradient để biết cách thoát ra khỏi điểm đó.
Ngoài ra, khi đứng trước nhiều mô hình khác nhau và cần chọn ra mô hình tốt nhất, các kỹ thuật thống kê sẽ giúp bạn kiểm định giả thuyết và đánh giá hiệu suất một cách khoa học, chính xác. Để làm được những điều đó, bạn cần trang bị kiến thức nền vững chắc từ những lĩnh vực toán học giữ vai trò then chốt trong Khoa học dữ liệu.
- Những lĩnh vực toán học then chốt trong Khoa học dữ liệu
- Đại số tuyến tính (Linear Algebra)
Hình 3. Đại số tuyến tính trong biểu diễn và xử lý dữ liệu
Đại số tuyến tính là xương sống của hầu hết các thuật toán máy học và học sâu (Deep learning), với nhiều khái niệm cốt lõi đóng vai trò thiết yếu trong việc xử lý và biểu diễn dữ liệu. Chẳng hạn, vector và ma trận được sử dụng để biểu diễn dữ liệu nhiều chiều như hình ảnh, văn bản hay các đặc trưng đầu vào; các phép toán như nhân ma trận, chuyển vị và tìm ma trận nghịch đảo được dùng trong việc biến đổi không gian dữ liệu nhằm phục vụ cho việc huấn luyện và tối ưu mô hình. Đặc biệt, các khái niệm như giá trị riêng và vectơ riêng là nền tảng quan trọng trong kỹ thuật giảm chiều dữ liệu PCA (Principal Component Analysis), giúp rút gọn thông tin nhưng vẫn giữ được các đặc trưng chính của dữ liệu. Trong thực tiễn, nếu bạn làm việc với mạng nơ-ron (Neural Networks), thì mỗi lớp trong mạng đều là một tổ hợp các phép toán ma trận phức tạp, cho thấy tầm quan trọng không thể thiếu của đại số tuyến tính trong lĩnh vực này.
- Giải tích (Calculus)
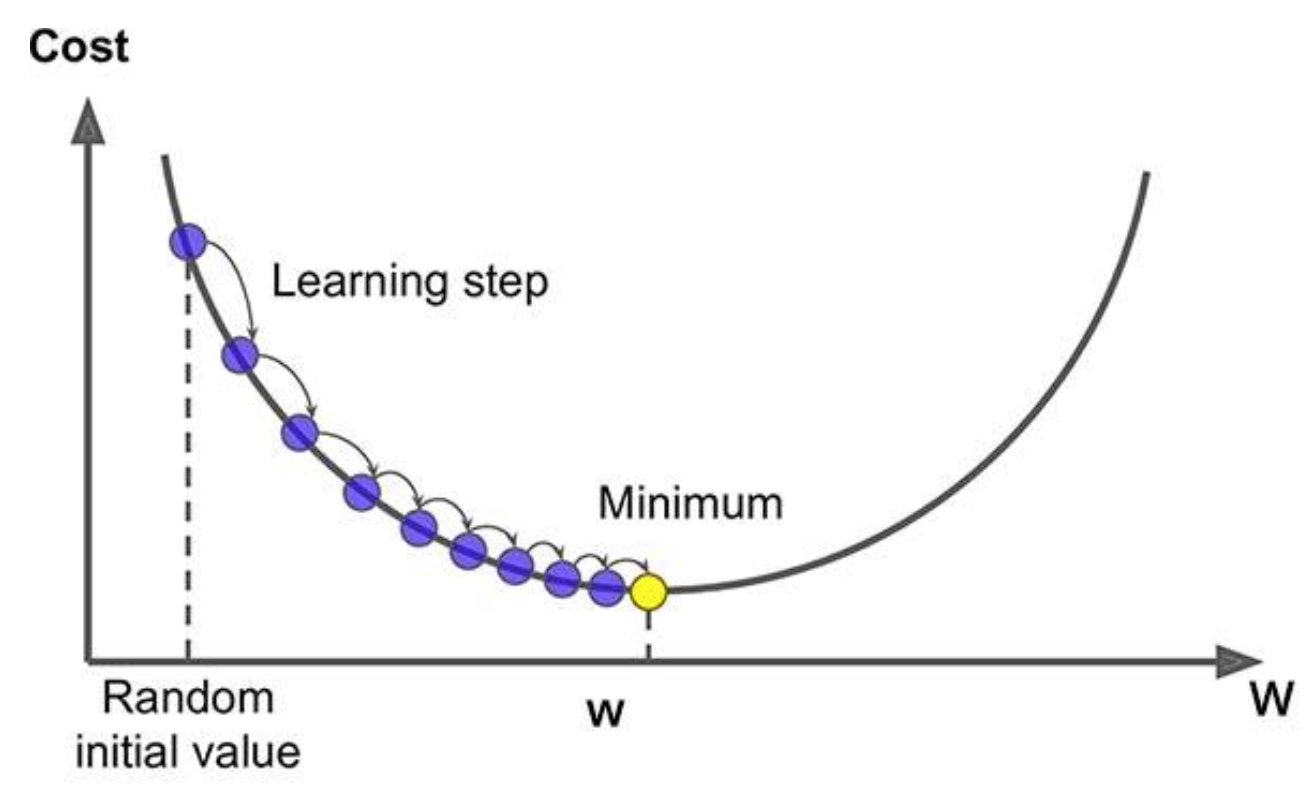
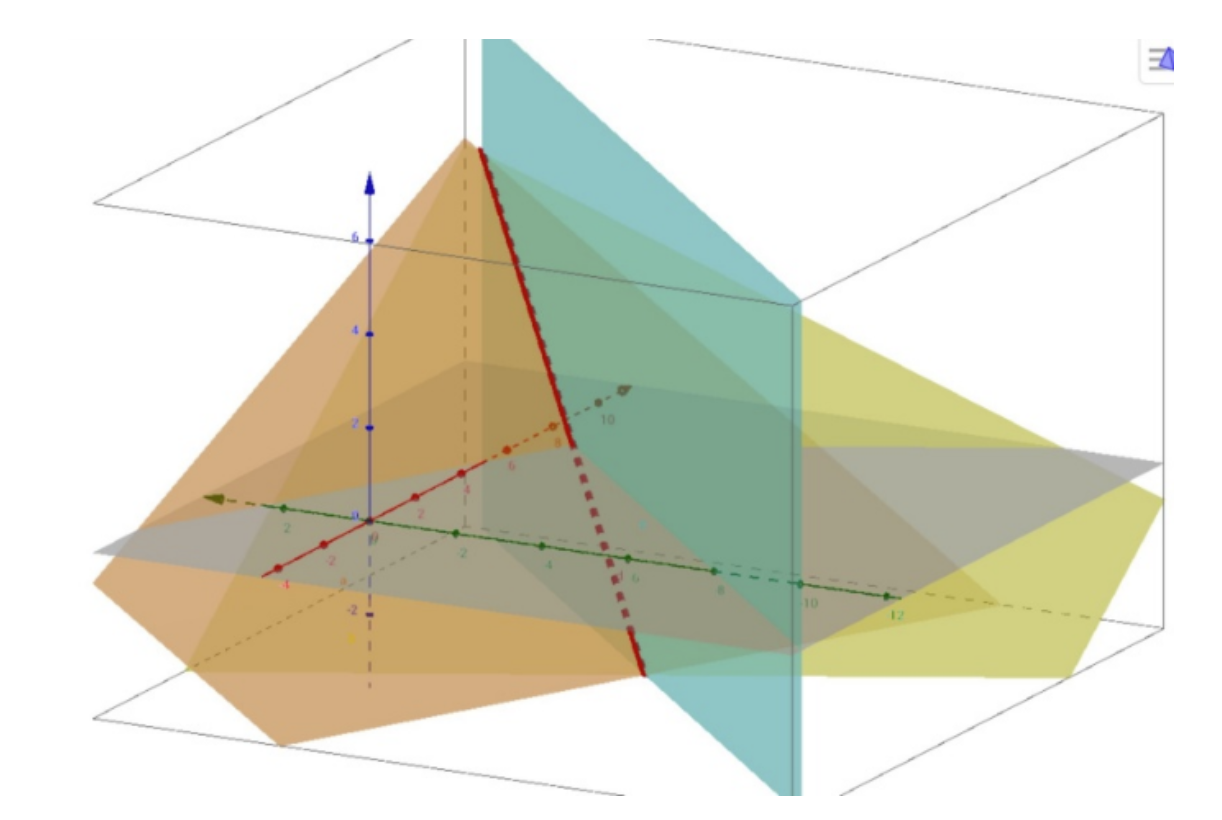
Hình 4. Gradient descent trong tối ưu hóa
Giải tích, đặc biệt là đạo hàm và đạo hàm riêng (partial derivatives), đóng vai trò quan trọng trong quá trình huấn luyện mô hình bằng cách tối ưu hóa hàm mất mát (loss function). Đạo hàm giúp xác định tốc độ thay đổi của hàm số theo từng biến đầu vào, từ đó cho biết nên điều chỉnh trọng số của mô hình theo hướng nào để giảm sai số. Một ứng dụng nổi bật của giải tích là thuật toán Gradient Descent – một phương pháp phổ biến sử dụng đạo hàm để tìm cực tiểu của hàm mất mát, giúp mô hình học tốt hơn qua từng vòng lặp. Bên cạnh đó, kiến thức về hàm số nhiều biến cũng rất cần thiết trong các mô hình phức tạp có nhiều tham số, chẳng hạn như hồi quy logistic (logistic regression) hoặc các mạng học sâu, nơi mà việc tối ưu hóa phụ thuộc vào nhiều chiều dữ liệu cùng lúc.
- Xác suất và Thống kê (Probability and Statistics)
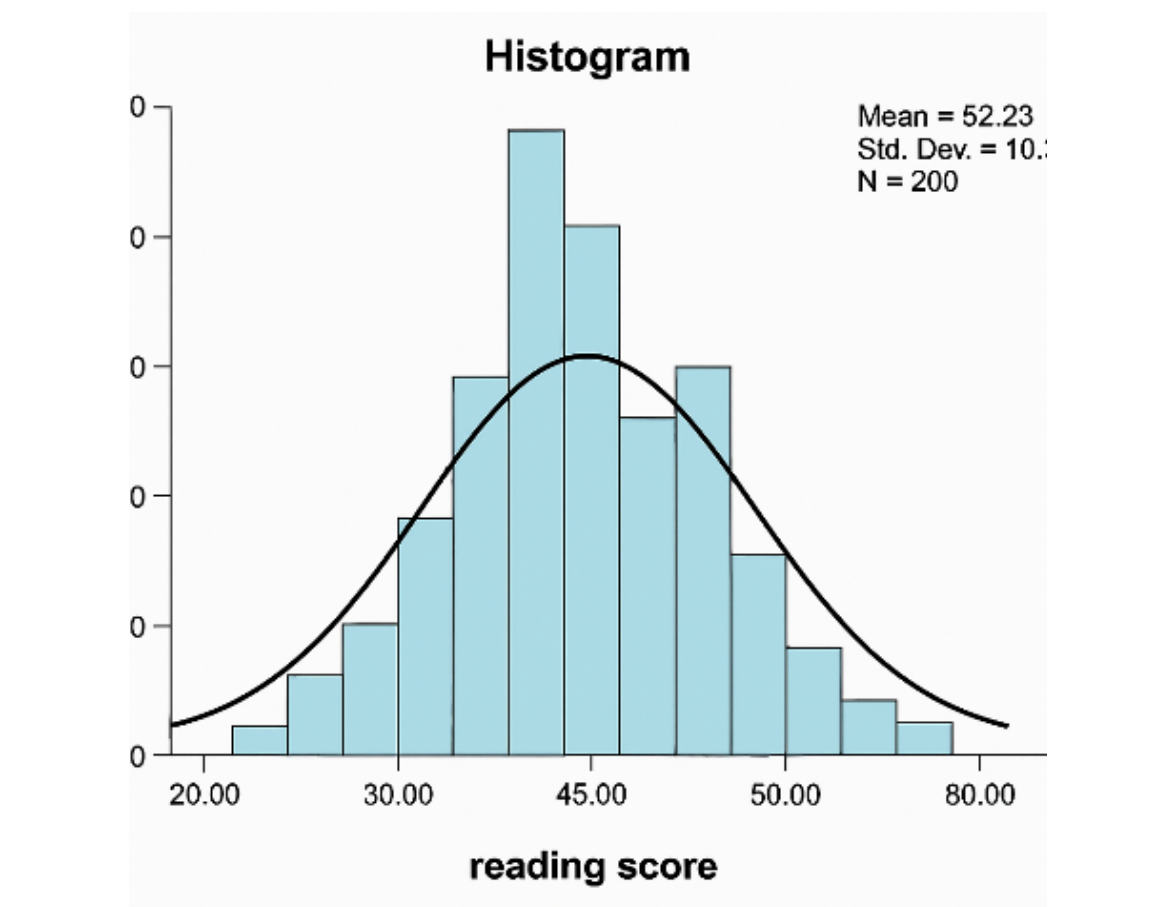
Hình 5. Một kết quả phân phối chuẩn trong SPSS
Xác suất và thống kê là những công cụ then chốt giúp chúng ta hiểu, mô tả và dự đoán dữ liệu một cách khoa học và có hệ thống. Kiến thức về xác suất cho phép dự đoán khả năng xảy ra của một sự kiện, chẳng hạn như trong bài toán phân loại email rác hay không rác. Các khái niệm như biến ngẫu nhiên và phân phối xác suất được ứng dụng trực tiếp trong các mô hình như Naive Bayes hay Hidden Markov Models, nơi dữ liệu có tính bất định cao. Thống kê mô tả, với các chỉ số như trung bình, phương sai, độ lệch chuẩn, giúp ta nắm bắt được đặc điểm tổng thể của dữ liệu đầu vào. Trong khi đó, thống kê suy luận lại hỗ trợ việc kiểm định giả thuyết (ví dụ A/B testing), ước lượng tham số, và thực hiện các phân tích hồi quy để đưa ra dự đoán hoặc quyết định trên tập dữ liệu mẫu. Đặc biệt, khi làm việc với dữ liệu thực tế – vốn thường đầy nhiễu, thiếu sót và không hoàn hảo – thì khả năng sử dụng xác suất và thống kê một cách linh hoạt sẽ giúp bạn khám phá ra những câu chuyện, xu hướng và mối quan hệ ẩn giấu đằng sau những con số tưởng chừng như vô nghĩa.
- Tư duy logic và Toán rời rạc (Discrete Math & Logic)
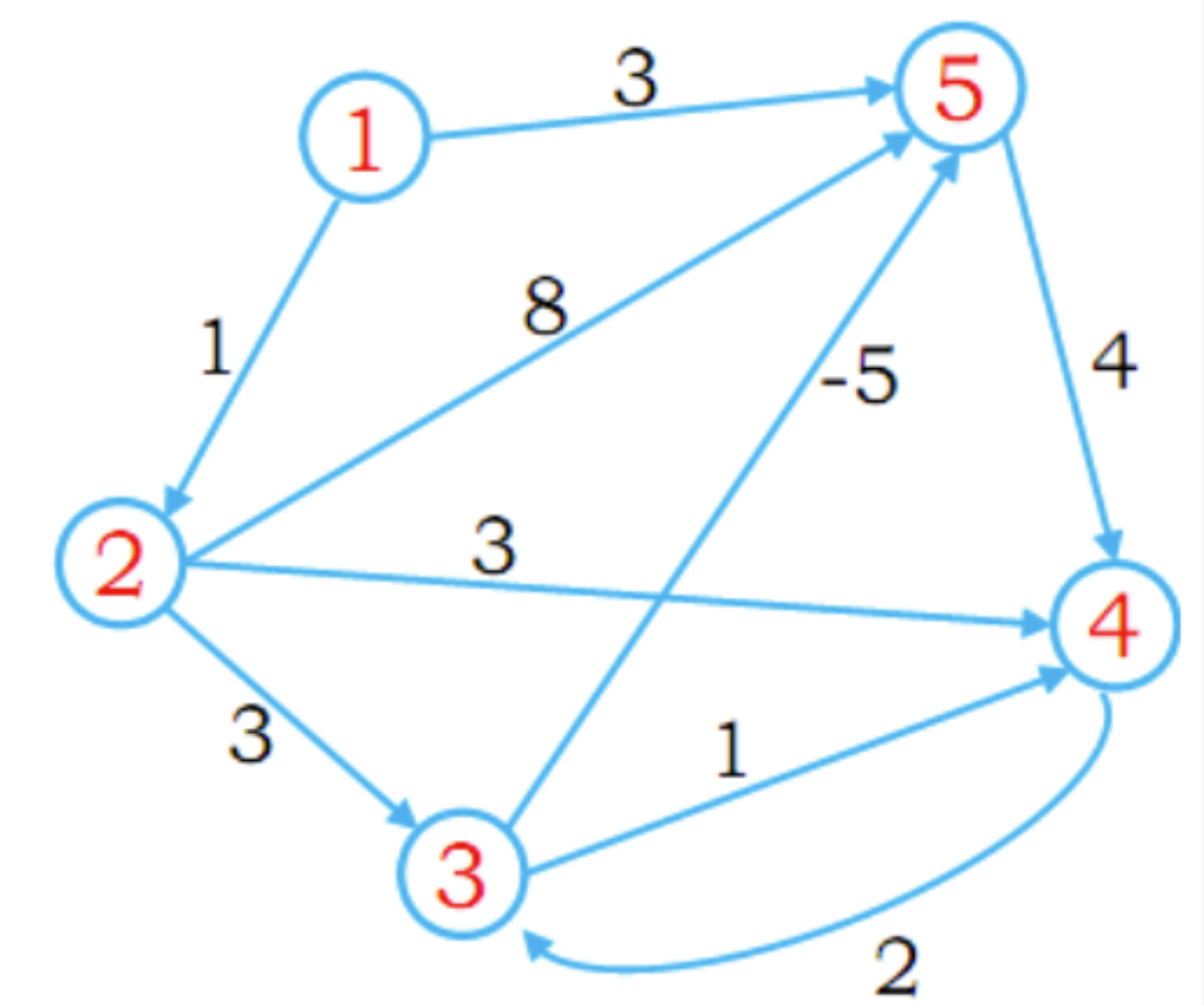
Hình 6. Một đồ thị có hướng trong toán rời rạc
Toán rời rạc bao gồm các lĩnh vực như lý thuyết tập hợp, tổ hợp, đồ thị và logic, đóng vai trò rất quan trọng trong việc thiết kế thuật toán, xây dựng cây quyết định, phân tích mạng xã hội cũng như khai phá dữ liệu. Các cấu trúc như cây nhị phân (binary tree) và đồ thị (graph) thường được sử dụng trong việc xây dựng cây quyết định hoặc triển khai các thuật toán tìm đường ngắn nhất – những bài toán phổ biến trong học máy và tối ưu hóa. Khái niệm tập hợp và ánh xạ đặc biệt hữu ích khi thao tác với tập dữ liệu lớn, hoặc xử lý các vấn đề về dữ liệu thiếu và trùng lặp. Bên cạnh đó, logic mệnh đề giúp xây dựng các truy vấn dữ liệu phức tạp, xác định điều kiện phân loại, và viết các câu lệnh điều kiện một cách chính xác trong ngôn ngữ lập trình. Chính vì vậy, toán rời rạc là nền tảng không thể thiếu để giải quyết nhiều vấn đề trong Khoa học Dữ liệu một cách hiệu quả và có hệ thống.
- 3. Kết luận
Toán học là nền móng của Khoa học dữ liệu – không thể thay thế bằng công cụ hay thư viện mã nguồn mở. Nếu bạn muốn làm chủ công nghệ, sáng tạo mô hình mới, tối ưu hóa hiệu suất hoặc giải thích kết quả cho các bên liên quan, thì kỹ năng toán học sẽ là “vũ khí” quan trọng nhất.
Học toán không chỉ để hiểu mô hình, mà còn để trở thành một người phân tích có tư duy – biết đặt câu hỏi, biết giải thích và biết ra quyết định từ dữ liệu. Xin giới thiệu đến bạn một số khóa học miễn phí trên Coursera như sau:
* Mathematics for Machine Learning and Data Science specialization
link: https://www.coursera.org/specializations/mathematics-for-machine-learning-and-data-science,
* Data Science Math Skills
link: https://www.coursera.org/learn/datasciencemathskills/home/module/5
ThS. Lê Thị Nhẫn
 fit@ntt.edu.vn
fit@ntt.edu.vn 028 71080889
028 71080889